💡 "[K-MOOC] 실습으로 배우는 머신러닝"을 수강한 내용을 바탕으로 작성된 글입니다.
최적화와 모형 학습
🔎 Machine Learning and Optimization
- 머신러닝 모델은 파라미터를 조정하여 loss를 최소화하면서 함수를 최적화 함
- Learning(학습) : 머신러닝 함수를 최적화하는 과정
- [예시] Linear Regression으로 학습해보기





🔎 Loss Function of Neural Networks
- Nerual Network는 알아내야 하는 파라미터의 갯수가 굉장히 많음
(아래의 그림에서 모든 회색선에 각각 하나의 파라미터가 필요)
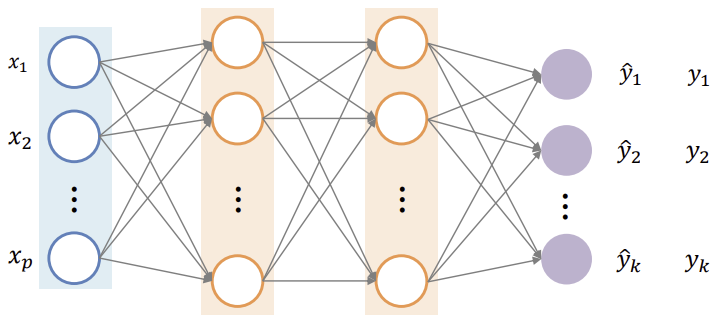
- 최적값을 알아내야 하는 파라미터의 갯수가 많아짐에 따라 손실함수의 그래프가 복잡해지고 고차원이 됨

🤔 복잡한 손실함수 내에서 어떤 파라미터 조정 방식을 사용하여 최솟값를 어떻게 찾을지 의문점이 발생 !
경사하강법
🔎 Gradient Descent 란?
- 함수의 기울기(Gradient)를 구하고 기울기의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것
[Gradient 방향] 함숫값을 올려주는 방향
[Gradient 반대 방향] 함숫값을 줄여주는 방향
(ex) x = W에서 기울기가 양수라면 극값은 W보다 작은 값의 x에서 존재하므로 현재 위치보다 음수쪽으로 이동해야함

🔎 Parameter Update 수식 유도
[1] 임의의 위치에서 급수전개를 활용해 알지못하는 손실함수를 근사적으로 2차 다항식으로 표현
(Quadratic approxiamation)
✅ Brook Taylor의 급수 전개 : 모든 일반적인 함수들은 무한대에 수렴하는 다항식으로 근사가 가능하다 !
✅ 급수전개를 활용한 Quadratic approxiamation 공식 (x=xo의 위치에서)

💡 파라미터 W = Wc일 때 손실함수 L(W)의 Quadratic approxiamation = La(W)
( 여기서 tc는 L(W)를 두번 미분한 함수에 Wc를 대입해 나온 값의 역수 )

[2] 위의 이차함수 La(W)를 W에 대해 미분하여 미분값이 0이 되는 지점을 찾으면 W = Wc - tc * ▽L
✅ 이 지점으로 W를 업데이트 !
✅ -▽L : 기울기의 반대 방향으로 이동 !
✅ tc : 이를 조정하여 step size를 조정할 수 있음 ! ( 관련 자세한 내용은 아래에서 다룰 예정 )

🔎 Gradient Descent 과정 그래프


경사하강법 심화
🔎 Learning Rate
- 위에서 구했던 손실함수의 Quadratic approxiamation (2차 다항식 근사) 함수는 W에 대한 2차 함수
- 이차항의 계수는 1 / tc
✅ tc에 따라 Quadratic approxiamation의 그래프 모양이 달라지며,
현재 위치에서 Quadratic approxiamation의 극솟값까지의 길이가 달라짐
✅ tc에 따라 실제 손실함수의 극솟값으로 다가가는 길이가 조절되고 이에 따라 학습 속도가 달라짐
💡 tc를 "Learning rate" 혹은 "Step size"라고 함

- Learning Rate가 너무 적을 때 극솟값에 도달하지 못하고 학습이 멈출 수 있음 / 학습속도가 느림

- Learning Rate가 너무 클 때 Loss값이 발산할 수 있음

🔎 Stochastic Gradient Descent
- Gradient Descent(GD)의 단점
: 모든 데이터에 대해 손살값을 계산하기 때문에 계산량이 너무 많음 - Stochastic Gradient Descent(SGD) 이란?
: 데이터셋을 쪼개 한 Batch에 대해서 손실값을 계산해 연산량을 줄이는 방법

- 그래프로 보는 GD와 SGD의 차이
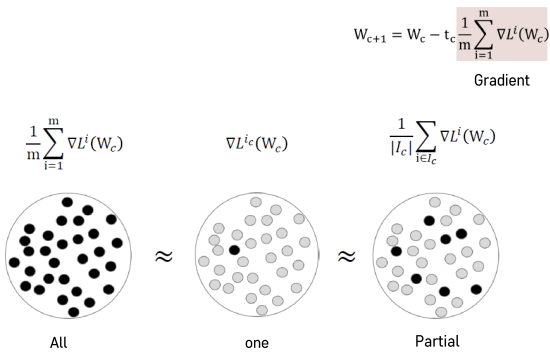

✅ 여기서 관측치 한개만 선택하는 방법은 부정확도가 크므로
메모리가 가능한 선에서 가장 큰 Batch size를 선택하는 것을 추천 !

🔎 Global Minimum & Local Minimum
- Global Minimum : Local Minimum에서 제일 작은 값

🔎 Momentum
- 관성적인 법칙에 따라 왔었던 방향으로 더 밀어주는 것
✅ Saddle point와 Local minimum에서 탈출할 수 있음
➕ Saddle point : 극솟값은 아니지만, 미분값이 0인 지점 (ex) 변곡점

- 수식
: 파라미터를 업데이트 할 때, 전의 Momentum도 고려하도록 μVc-1을더해줌

🔎 출처
https://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95
경사 하강법 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 경사 하강법(傾斜下降法, Gradient descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동
ko.wikipedia.org
http://www.mit.edu/~hlb/StantonGrant/Lecture10/origins.pdf
'2022년 > [K-MOOC] 실습으로 배우는 머신러닝' 카테고리의 다른 글
| [3주차] Classification (0) | 2022.11.22 |
|---|---|
| [2주차] Machine Learning Pipeline (0) | 2022.11.21 |
| [1주차] Intorduction to Machine Learning (1) | 2022.11.21 |