💡 "[K-MOOC] 실습으로 배우는 머신러닝"을 수강한 내용을 바탕으로 작성된 글입니다.
머신러닝 분류 모델링
🔎 Bias-Variance Tradeoff
- Bias : 치우쳐져 있는 정도 / 실제 값에서 우리가 예측한 값이 얼마나 떨어져 있는가?
(ex) Train Dataset에 대해 Bias가 너무 작으면 과적합 우려가 있음 - Variance : 변동성 / 모집단에는 많은 샘플 데이터셋이 존재 → 각 샘플마다 학습된 모델에 차이가 존재
(ex) train에 과적합되면 변동성이 커지기 때문에 Test에 대해서는 예측을 잘못할 수 있음
✅ 모델의 모형이 Train Dataset에 대해 Bias가 크면 Variance가 작아지는 경향이 있음
반대로 Bias가 작으면 Variance가 커지는 경향이 있음
✅ 모형의 오차 = Bias + Variance
🔎 Hyperparameter
- Hyperparameter 조정을 통해 모델의 복잡도를 통제할 수 있음
✔ 가장 좋은 성능을 낼 수 있는 모델을 학습하기 위해 최적의 Hyperparameter를 결정해야 함

🔎 Validation Set
: 좋은 모델을 선택하기 위한 검증 데이터 셋

🔎 Classification
- 범주형 종속변수 : Label, Class
- 분류 문제 예시
# 제품의 불량 여부
# 고객의 이탈 여부 - 특정 모델이 모든 경우에 대해 항상 좋은 성능을 낸다는 보장이 없으므로,
문제 상황에 따라 적절한 모델을 선택하야 함
KNN
🔎 K-Nearest Neighbors
- 가정 : 두 관측치의 거리가 가까우면 Y도 비슷하다
- K개의 주변 관측치의 Class에 대한 majority voting (다수결)
- Distance-based model / instance-based learning
- 예시
: 아래의 그림처럼 K=3이면 ★은 Class B로 판단되고, K=6이면 ★은 Class A로 판단됨

🔎 거리
- 범주형 변수 : 거리를 측정할 수 있도록 Dummy Variable로 변환
- 거리 측정 방법
1) Euclidean 2) Manhattan 3) Minokowski

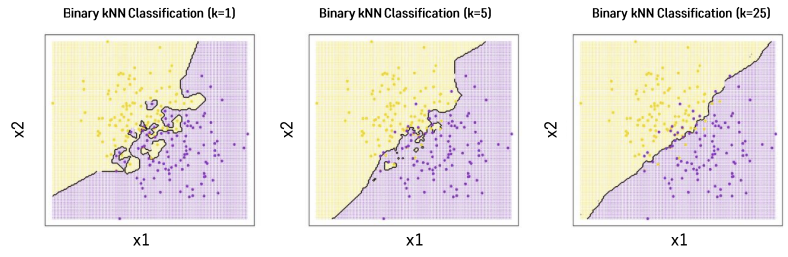
🔎 K의 영향
- K : KNN의 Hyperparameter
- K가 클수록 Underfitting / K가 작을수록 Overfitting
✅ Validation dataset을 이용해 최적의 K를 결정해야 함
Logistic Regression
🔎 Logistic Regression란?
- Logsitic Function(=Sigmoid Function)을 사용하는 Linear Regression
- Linear Regression의 Output에 변환함수로 Logistic function을 활용
➕ Linear Regression : 수치형 설명변수 X와 종속변수 Y간의 관계를 선형으로 가정하고
이를 가장 잘 표현할 수 있는 회귀 계수를 추정하는 방식
🔎 Logistic Regression의 필요성
- 분류 문제에 Linear Regression을 적용할 경우 Y의 범위가 다른 문제점이 발생 (오차 상당히 커짐)

🔎 Logistic Regression의 목적
- 분류문제에 대해 회귀식의 형태로 모형을 추정하는 것
🔎 Logistic Regression 특징
- Y에 대한 Logit function을 회귀식의 종속변수로 사용
- Logit function은 설명변수의 선형 결합으로 표현됨
- Logit function의 값은 종속변수에 대한 성공확률로 역산될 수 있기 때문에 분류 문제에 적용 가능
🔎 이항 Logistic Regression
- 종속변수(y)가 이진형(0/1)의 형태를 갖을 때 사용
- 확률값이 0.5를 초과할 때 '1'로 분류하고 0.5이하이면 '0'으로 분류
- 이진분류이기 때문에 하나의 class에 대한 확률값p를 알면 나머지 class는 1-p확률을 가짐을 알 수 있음
- Logistic function (= Sigmoid function)


- 이항 Logistic Regression 함수
: Linear regression의 식을 Logistic function의 입력값(x)으로 넣은 함수
: Linear regression의 값을 확률값으로 바꾸어 주는 과정


- Logistic Regression의 Loss Function
- Cross-Entropy Loss
✔ i : 관측치 행
✔ j : class
✔ Class(i,j) : i번 관측치의 실제 j클래스일 확률
✔ f(i)(x(j)) : i번 관측치가 j클래스로 분류될 확률값
- Cross-Entropy Loss


🔎 다중 Logistic Regression
- 구분해야할 클래스가 3개 이상일 때 사용
- 이항 Logistic Regression과 다른 점 : 확률로 변환시켜주는 함수를 Sigmoid 함수가 아니라 Softmax Function을 사용
- Softmax function
- 여러 개의 선형 방정식의 출력값을 0~1 사이로 압축하고
모든 클래스의 확률을 더했을 때 1이 되도록 만들어주는 함수
- 여러 개의 선형 방정식의 출력값을 0~1 사이로 압축하고
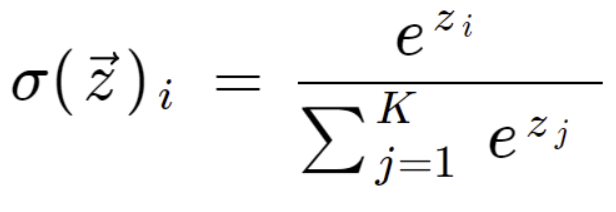
🔎 출처
https://blog.naver.com/PostView.naver?blogId=psycomaniac&logNo=222472359036
다중 분류 로지스틱 회귀분석(feat.소프트맥스)
※ 해당 카테고리에 있는 문제와 문제풀이 방식은 「혼자 공부하는 머신러닝 + 딥러닝」(박해선, 한빛미디...
blog.naver.com
https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B7%B8%EB%AA%A8%EC%9D%B4%EB%93%9C_%ED%95%A8%EC%88%98
시그모이드 함수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 시그모이드 함수는 S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수이다. 시그모이드 함수의 예시로는 첫 번째 그림에 표시된 로지스틱 함수가 있으며 다음
ko.wikipedia.org
'2022년 > [K-MOOC] 실습으로 배우는 머신러닝' 카테고리의 다른 글
| [4주차] Model Learning with Optimization (0) | 2022.11.22 |
|---|---|
| [2주차] Machine Learning Pipeline (0) | 2022.11.21 |
| [1주차] Intorduction to Machine Learning (1) | 2022.11.21 |